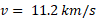Escape velocity equation
There is an equation to work out escape velocity of a gravitational field, which is how fast a mass must travel to escape the field. When the equation gives the object negative potential energy it has escaped the gravitational field.
This is deriving the escape velocity from equations we have looked at before and using kinetic energy equation:
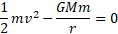
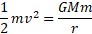
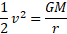
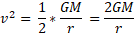
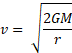
Example of Earth's escape velocity
We can work out the escape velocity of earth using the escape velocity equation. For this example, we will ignore air resistance but for any given mass the escape velocity can be worked out as the following (units will be included during working out to show how the various units cancel and have a more comprehensible view):
G (gravitational constant) = 6.67408 x 10-11 m3 kg-1 s-2
r (radius of Earth/distance from centre of mass to surface) = 6371 km
M (mass of Earth) = 5.9722 x 1024kg
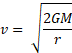
Input the values we have into the standard equation and multiply r by 1000 to get meters as G is also using meters:
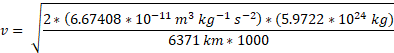
Multiply all parts of top part of fraction to get overall units for one number:
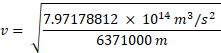
Complete the rest of the equation cancelling units when needed:
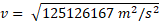
Escape velocity from the surface of the earth:
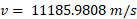
You can now divide that by 1000 to get units in km for easier understanding: